No Limit Poker Pot Odds

Posted By admin On 11.05.21

Poker Pot Odds Chart

Learning how to calculate the odds of winning a poker hand is essential for every player. In this article we'll provide you with some techniques that you can use to calculate the odds of winning a poker hand on the fly, we'll equip you with a tool that can do that for you and provide you with some useful information that you can memorize.

Apr 14, 2019 Poker has a lot of mathematical elementsbut pot odds are the most important. A solid understanding of pot odds will allow you to play draws better, go all-in preflop & postflop, and handle a wide range of decisions with ease. Pot odds evaluation. Although upon first glance pot odds may appear difficult, it is one of the most basic applications of mathematics in the game of poker. If you base your drawing decisions on pot odds, then you will mathematically be a winner in the long run, regardless of whether or not you win the hand or not.

Poker Odds and Outs Calculations

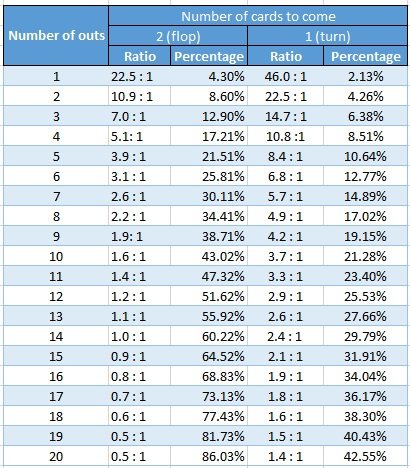
Poker Pot Odds Chart

Let's start with the basics. With the exception of the very strong holdings like some flushes, quads etc. almost every poker hand can improve. Outs are the cards that will improve your hand if they show up at a later street. For example, if you're holding AQ on a Q34 board you can still improve to two pair or trips if you hit on of the three Aces remaining in the deck or one of the two remaining Queens.

How do we know if one of our opponents isn't holding one of those cards? Well... we don't and that's why we're forced to ignore that possibility in our calculations.

Here are some common examples of drawing hands in no-limit hold 'em and the number of outs that they can hit to improve:

Gutshot Straight Draw (examples: JT on Q93, 57 on 69A etc.) - 4 outs
Open Ended Straight Draw (examples: 98 on T72, KQ on JT5) - 8 outs
Flush Draw (examples: AhQh on 2c7h9h, 4d6d on JdKd8s) - 9 outs

Pot Odds

Pot Odds - the size of the pot in relation to the bet that you have to call to continue playing the hand. Pot Odds are usually represented in the form of a ratio (2:1, 3.2:1, 4:1 etc.). Pot odds are essentially the risk you have to take (call) to gain the reward (size of the pot).

Let's say that the size of the pot on the flop equals 2$. Our opponent is betting 1$. To continue playing we have to call 1$ and if we do we can win 2$ + 1$ = 3$. We're getting 3 to 1 pot odds. Now let's make it a bit more complex, pot size is 3,55$, opponent bets 2,33$. We have to call 2,33$ to win 3,55$ + 2,33$ (5,88$). Our pot odds are 5,88$ / 2,33$ = roughly 2.5 : 1.

If you've ever watched televised poker you probably remember that it's common to use % value when determining the chance of winning a poker hand. That's why it's really handy to be able to convert the ratio (used to represent Pot Odds) into % (used to represent equity which is basically a share of the pot that belongs to us at certain point in a hand based on our chance of winning that hand).

Here's an easy way to do that:

Let's say our opponent is betting 2$ into 6$ pot so our pot odds equal 4:1. To convert the ratio into % add both sides of the ratio (4 + 1) and use that number as a divisor for the right part of the ratio (1 / 5 = 20%).

In the example above you need to win 20% of the time to break even when your opponent is giving your 4:1 pot odds. How often do you need to win to make the call in other popular situations? Here are some examples for you to memorize:

1:1 = 50%
2:1 = 33%
3:1 = 25%
4:1 = 20%

Rule of 2 and 4

Now that you know what pot odds and odds are you can learn the quick way of calculating the percentage chance of your hand improving. It's called the rule of 2 and 4 and it's very simple:

With one more card to come (on the flop waiting for the turn or on the turn waiting for the river) multiply your outs by 2 to calculate the % chance of your hand improving. With two more cards to come (opponent all-in on the flop or any other situation when you have to call just one bet to see both turn and river) multiply your outs by 4 to calculate the % chance of your hand improving.

Example: You're holding T8 on a J24 board, you have 9 outs to hit your flush. Villain goes all in on the flop. Your % chance of improving to a flush equals 4 * 9 = 36%. Let's consider the same situation but this time flop went check/check, the turn is an Ace of clubs and your opponent is betting. Your % chance of improving in that situation would be 2 * 9 = 18%.

Rule of 2 and 4 is fairly accurate when it comes to no-limit hold'em. If you have 9 or fewer outs you should never be off by more than 2% in your calculations when using this rule and it's very rare to flop more than 9 outs in no-limit hold'em. That being said you probably don't want to make those calculations every single time and it's a very good idea to memorize some common situations that can occur at the tables.

Hand vs. Hand All-in Pre-flop

	Example	Odds	%Odds/Equity
Pocket Pair vs. Smaller Pocket Pair	AA vs. TT	4 : 1	80%
Pocket Pair vs. Two High Cards	88 vs. AQ	1.2 : 1	55%
Pocket Pair vs. Two Low Cards	QQ vs. 67	4.9 : 1	83%
Pocket Pair vs. High Card and Low Card	JJ vs. A9	2.3 : 1	70%
Two High Cards vs. Two Low Cards	AJ vs. 78	1.9 : 1	65%
High Card and Low Card vs. Unpaired Hand	AT vs. KQ	1.2 : 1	55%

Odds of Improving Post-flop

	Example	Outs	Flop%/Odds	Turn%/Odds
Gutshot Straight Draw	JT on Q83	4	16.5%/5.1 : 1	8.7%/10.5 : 1
Two High Cards	AK on 962	6	24%/3.1 : 1	13%/6.7 : 1
Open-Ended Straight Draw	89 on A76	8	31.5%/2.2 : 1	17.4%/4.7 : 1
Flush Draw	AhQh on Jh5h8c	9	35%/1.9 : 1	19.6%/4.1 : 1
Flush Draw + High Card	As2s on 8sQs4d	12	45%/1.2 : 1	26.1%/2.8 : 1
Open-Ended Straight Flush Draw	Td9d on Jd8dKh	15	54.1%/0.85 : 1	32.6%/2.1 : 1

Poker Odds Calculator

So far you've learned about outs, odds, calculating the chance of improving your hand on the fly, and figuring out if it's profitable to make a call based on the pot size and bet size of your opponent. That's enough to get you started, but it probably doesn't answer every question you might have.

Maybe you want to figure out what's the equity of your set vs. two opponents holding a flush draw and straight draw? Maybe you want to know if your hand has any chance of winning in a 5-way family pot. Fortunately, we got you covered! You can answer those and many other questions using the Odds Calculator provided below:

If the Odds Calculator is not displaying, please check your browser settings and enable scripts.

Here's a quick guide on how to use the odds calculator:

In the top right, you can choose your preferred game (you can even calculate the equity of winning a hand in games like Omaha Hi/Lo or Razz).
Choose the number of players in the pot.
Click on player's hole cards and assign them using the list provided at the bottom of the calculator.
You can add cards to the board in the same way.
Click 'Get Odds' et voila!

Now you can calculate the odds of winning any poker hand. With such a powerful tool at your disposal, you'll improve as a poker player in no-time!

Golproductions